从这两个软件本身来讨论他们的区别,@徐尤熙的回答已经是非常到位。
而作为一名程序狗的我,想好好地给大家解释一下矢量图形和位图的区别。
很多人对图形和位图的理解就是,矢量图可以无限放大而不失真,位图放大到一定程度之后就会越来越模糊。现在不能无限放大都快成数字图像的原罪了。那么你有没有想过,既然矢量图这么牛X,我们日常生活中的照片、海报等常见的图像为什么不使用矢量图形的格式来保存呢?
让我们来看看这两种格式到底都是什么东西,区别在哪。
首先说图形,也时候也被称作矢量图形。
图形这个词大家应该都不会陌生,从小学开始,我们就开始接触一些简单的图形,如矩形、三角形、梯形等。不要怀疑,这些东西就是图形,就这么简单。
上过初中的同学应该都知道,有个东西叫平面直角坐标系,也叫笛卡尔直角坐标系,在这样的一个概念之下,我们可以清晰、量化地表示点、线、面。
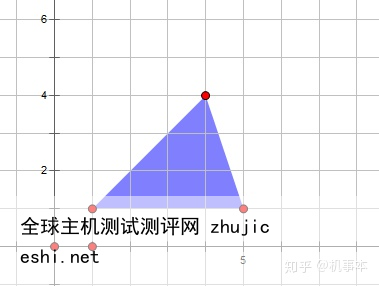
比如,我画了如下的这样一个三角形,它的三个顶点坐标分别是(1,1),(5,1),(4,4)。
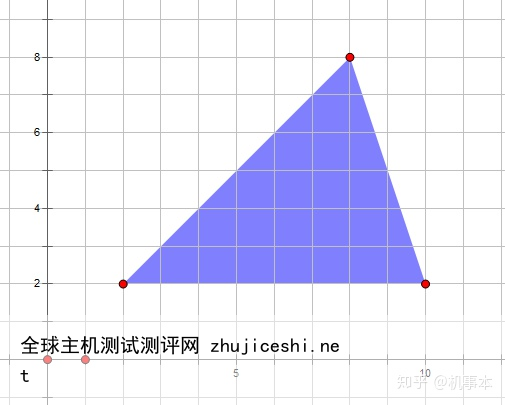
这个时候,如果我将这三个点的x、y坐标同时乘以2,使得他们变成(2,2),(10,2),(8,8),于是这个三角形就变成了下面这个样子。
通过一些简单的定理就可以证明这个三角形和原来的三角形是相似的,也就是说,按照我们通常所理解的“形状”一词,这两个三角形的形状是完全相同的,面积是原来的4倍。
也就是说,根据这个三角形三个顶点的坐标信息,我们现在就可以任意地对这个三角形进行放大和缩小操作,而不会改变这个三角形的形状。无非就是把坐标乘以不同的系数呗。
如果这个图形变得复杂一些,那么我们可以将他们分解为若干个三角形或者其他形状的组合,除了需要保存的坐标信息多了一些之外,变换的原理并没有发生多大的变化。
上面举这个例子,大致可以理解为所谓的“矢量图形”在计算中保存和显示的原理,当然了,细心的同学可能也发现了,上面这种简单粗暴的将坐标乘以一个系数的方法会导致图形位置发生变化,在此只是为了简单地说明原理,所以使用了一种尽可能简单的计算方法来进行演示。
具体实现的时候,还需要涉及到一些向量(也叫矢量)的知识。这也是为什么计算机图形常常被称为矢量图形的原因。
(相信点进这个问题来的人也不会想听我在这大讲数学。所以矢量方面的具体知识在这就不谈了,这个在高中数学和高等数学中均有涉及,感兴趣的同学请自行学习或复习。)
讲到这,还有个问题没解决,那就是曲线。直线好说啊,两点确定一条线段,曲线总不可能无线分割然后把每个点的坐标保存起来。
说到这,我们就不得不感谢两个人,一个是法国(fà gúo)的一名数学家保尔·德·卡斯特里奥(Paul de Casteljau),一个是同在法国的一名工程师皮埃尔·贝塞尔(Pierre Bézier)。
皮埃尔·贝塞尔前者发明了一种算法,可以通过很少的控制点,去生成复杂的平滑曲线,而后者将这种曲线应用在了汽车的车体工业设计当中,并且很热心肠地承担了对这种曲线的宣传工作。所以,后来这种曲线就以他的名字命名为了贝塞尔曲线,至于发明了贝赛尔曲线的数学家德卡斯特里奥,反倒是默默无闻了……
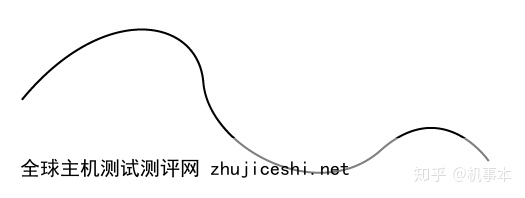
至于这个贝塞尔曲线,用过AI或者PS的人应该都见过。还记得被钢笔工具支配的恐惧吗 ,当我们用钢笔工具画曲线时,软件就会要求我们拉出一个个控制点,这样绘制出来的曲线,其实就是传说中的贝赛尔曲线。
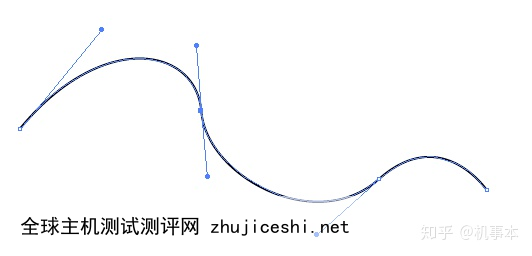
一条看起来很普通的曲线曲线和它的控制点们看到这里,想必大家也已经猜到了,计算机在保存这条曲线的时候,只需要保存几个控制点的信息,只要有这几个控制点的信息,计算机就可以保证显示出来的就是一条这个样子的曲线,而且通过这几个控制点的信息,计算机还可以实现对这条曲线进行无限放缩而不失真。
所以啊,计算中在保存图形时,实际保存的是一些可以用来生成相同图形的坐标、函数、向量等信息,这些信息的背后都是一些数学原理。就好比我告诉你一个二次函数: y=3x2+5x−6y=3x^2+5x-6 ,只要你学过初等函数,再把这个式子记下来,无论走到哪,只要有纸笔,你就能大致画出它的函数图像,而不用去刻意记忆这条线的样子,而且想画多大画多大。
接下来我们再来说图像。
图像也叫位图,是由一个个像素点构成的,图像的概念非常好理解,就像电视机屏幕上的一个个小像素点组合成一幅完整的画面,就像地上的彩砖一块一块组合起来形成五彩缤纷的图案。
红色和黑色的砖形成了一个菱形为了说明图像的保存原理,我在ps里新建了一个30x30像素的图像,试着画了一个和上面的三角形很像的三角形。
为了能看清每个像素的边界,我把背景涂成了黑色。
可以看到,所谓图像的大小是30x30,就是横竖各有30个像素点,单个像素点已经是图像的最小单位,每个像素只能被设定为一种颜色。计算机在保存这张图像的时候保存的就是这900个点的颜色信息。可以大致想象为这样:
第1行第1个像素:RGB(0,0,0)(即黑色)
第1行第2个像素:RGB(0,0,0)
……
第19行第9个像素:RGB(0,18,85)(上顶点左侧的深蓝色)
……
第30行第30个像素:RGB(0,0,0)
有人说了,我平时见到的图像不是这样一格一格的啊,那是因为你见到的图像分辨率比较高,比如我把上面这张图做放大处理,放大到300x300像素,它就变成了这样
虽然看起来舒服多了,但其实也就是横竖各300个点一共90000个点而已,之所以看起来舒服多了,是因为这个时候的单个点已经小到肉眼分辨不出来了。
可以想象,这样的保存方式就导致了一个问题,当图像的分辨率较高时,文件体积会变得特别庞大,保存几百个点、几千万个点可不是什么好玩的事情,所以这就催生出了各种压缩图像的方法,这是题外话。
另一个问题就是大家所熟知的,一张图像的分辨率是固定的,当我们想要查看图像的细节,而这个细节的精度已经超出图像分辨率所能表示的范围时,我们就只能看到万恶的马赛克了。
两种格式的基本原理已经说完了,接下来我们看看什么情况下应该用图形,什么情况下应该用图像。
大家应该有这样一种经验,如果我拿一张矢量图和一张照片放到你面前,你总是能一瞬间就区分出两者谁是谁。如:
相信大家一眼就能看出左边是照片,右边是矢量图。
为什么我们能做出这样的判断,我认为既不是因为这张矢量图中的颜色不如照片中的丰富,也不是因为它的饱和度比照片低,这只是我碰巧选到这两张图的问题。
真正的问题是:因为矢量图的背后都是数学算法和模型,所以呈现出来的画面总是有一定规律可循的,尽管我们不能一眼看透它背后的规律,但就是这样一种规律会给我们一种人造的、不真实的感觉。
比如上图中的湖水,从上到下有一个明显的双色渐变,远处的山,明显只使用了为数不多的几种颜色。当然,这些问题都可以想办法进行优化,比如,使用更为复杂的多层渐变对湖面进行着色,后面的山也是同理,不大的面积内用上几十层渐变,但是这样一来是会极大地增加作画成本,二来是无论我们使用多么精细的技术,总归是有规律可循的。比如说贝塞尔曲线,尽管看起来很圆滑很漂亮,背后终归是函数,是算法。
而照片天生没有这样的问题,湖面上水的波纹,你能找出一个函数公式完美的拟合吗?天上云彩的颜色、形状、云在水中形成倒影时明度的下降、水的波纹导致的形状的扭曲,这些都是用公式很难去表达,去计算出来的。更别说现实世界中的细节千千万万,我们随手一拍就是不同的风景。这才是矢量图和照片最大的不同。
所以,当我们需要一张有规律可循、中规中矩的图时,矢量图就是最好的选择。这方面的例子有很多,比如软件的图标:
对于软件的图标来说,我们就是需要简单明快的配色,有数学理论支撑的漂亮曲线,让人一眼就能认出来,那我们无疑应该选用矢量图进行绘画。
而当我们想要更多的细节、更加原汁原味的真实时,我们就应该选用图像,比如一个新闻记者,他肯定更愿意要一张高清彩色照片,而不是画家画的现场写生。
至于海报,则要视具体的内容而定。
事实上大部分情况下我们使用PS是因为我们已经有了一定的素材,需要使用其中的图像处理功能。如果是凭空作画,那么AI的矢量图形则是更好的选择。
参考资料:
[2]谈谈贝塞尔曲线 - 简书



















0 留言