霍普菲尔德于1982年发明了Hopfield网络,从那时开始,人们就将多种不同的神经网络模型组合在一起,互相比较,得到了较好的性能与鲁棒性。据我所知,由于Hopfield网络是Boltzmann机器和深度信念网络(DBN)的基础,因此在介绍Boltzmann机器和Deep Belief 网络的教材中,都会介绍Hopfield网络。
与当前热门的深度网络相比,Hopfield网络从不同的视角观察了人类的学习系统,值得我们一探究竟。让我们看看Hopfield网络得基本运作机理。
Hopfield网络基础及其运作方式
Hopfield网络的核心是,输入残缺的数据后,可以重建完整数据的一个模型。
我们可以将网络描述为使用链接连接节点(或称单元、神经元)的网络。每个节点在任何时间点为-1或1中的某个状态,我们可以使用向量V表示给定时间点,各个节点的状态。
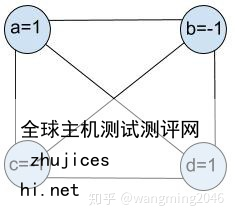
Hopfield网络是个全连接网络(即是个全连接的无向图),如图1所示,即每个节点都与其他节点连接,我们使用链接表示这种连接,因此这种链接是对称的,换句话说,节点i和节点j之间的链接是一样的,没有方向的区别,我们使用权重来表示各个节点之间连接的强度,因此,我们使用矩阵W来表示节点之间连接的强度(权重),我们可以很容易的知道这是对称矩阵。
图1:具有4个节点的Hopfield网络
我们可以使用以下V和W来表示这个网络。
我们如何才能得到权重矩阵W呢?首先,我们可以注意到节点不链接到自身,因此我们可以将权重矩阵的对角置为0。正如我们前面所知道,这是一个对称矩阵,即Wab=Wba, 我们可以将权重矩阵与节点的状态结合起来,即Wab=Va*Vb,这样我们就可以得到一个权重矩阵W, 如下式所示。这其实就是等一下我们要讨论的Hebbian学习规则。
现在,构建了权重矩阵之后,我们需要定义规则,确定每个节点的状态。由于节点的状态为(-1,1),因此我们制定了以下规则:
现在,让我们来看看Hopfield网络实际上如何工作。比如说,我们有残缺的V’=[1, -1, -1, -1],也就是最后一位反转了。我们可以使用V’初始化网络状态。
Figure 2: 残缺输入的Hopfield网络
我们可以使用先前制定的规则,更新网络状态,对于Va,我们有:
Va = f(wab · Vb + wac · Vc + wad · Vd) = +1
注意:尽管Vb和Vc都是-1,但是Wab*Vb 和Wac*Vc 对x的贡献为正值,反转的节点贡献为负值,这样所得到的Va为+1。换句话说,使用向前所构建的W,如果节点的状态与原本的状态相反,我们将迫使其转变到相反的状态,如果节点的状态与原本的状态一致,则停留在原来的状态。不同的状态互相排斥,相同的状态互相吸引。这是Hebbian学习规则的一种表述。
类似得:
Vb = f(wba ·Va + wbc · Vc + wbd · Vd) = -1
Vc = f(wca · Va + wcb · Vb + wcd · Vd) = -1
现在,对于反转的位,我们可以得到:
Vd = f(wda · Va + wdc · Vc + wdb · Vb) = +1
Va=+1吸引节点d,因此Wda*Va>0, 而Vc=Vd=-1,排斥节点d,因此总体上贡献了正值wdc · Vc + wdb · Vd >0。
原来相同的节点趋向于相同的状态,原来相反状态的节点排斥对方到相反的状态。这样我们修复了原始的V。
但是,是什么原理使得Hopfield网络可以运行呢?
到目前为止,我们发现,一旦网络完全确定了,也就是W和状态向量V确定了,这样我们恢复残缺的V,我们根据规则,更新网络状态即可。
换句话说,在使用V’初始化网络状态后,我们可以让网络使用以上规则进行演化,这样网络就可以收敛到先前的状态。不仅如此,当网络到达先前状态后,无论网络迭代多少次,网络的状态依然保持不变。
让我们来看看为什么吧?
我们可以定义一个函数,这个函数使用状态V和矩阵W作为自变量。我们将这个方程称为与网络状态相关的能量方程,将其表示为:
见证奇迹的时刻到来了。
结论1
如果节点Vi的状态从+1变为-1,我们将会得到:
现在,如果将Vi的状态从-1变为原来的+1,那么dVi=2, 这意味着xi为正数,也就是Delta能量为负,这样能量就是单调递减,直至到达最低点。
结论2
但是,是否存在最低点,或者能量将一直减小直到负无穷?
换句话说,我们要弄清楚,Delta能量是否可用为0。为了使Delta E =0,我们需要使dVi=0,也就是要Vi(k-1)’ = Vi(k)’,也就是前一状态的的Vi和后一状态的Vi相同。
让我们假设,Vi(k-1)’ = +1,我们要Vi(k)’ = +1,或者说 xi(k) > 0。
由于Vj(k-1)’ = Vj ,因此xi(k) 一直为正。
总之,我们证明了当状态恢复为原值时,能量方程不会再改变了。换句话说,dVi=0,节点不会更新到不同的值---系统到达了稳定的配置状态。
以下是Hopfield Network的源代码。
import numpy as np
from matplotlib import pyplot as plt
from random import randint, shuffle
class InvalidWeightsException(Exception):
pass
class InvalidNetworkInputException(Exception):
pass
class HopfieldNetwork(object):
def __init__(self, num_inputs):
self._num_inputs = num_inputs
self._weights = np.random.uniform(-1.0, 1.0, (num_inputs, num_inputs))
def set_weights(self, weights):
"""Update the weights array"""
if weights.shape != (self._num_inputs, self._num_inputs):
raise InvalidWeightsException()
self._weights = weights
def get_weights(self):
"""Return the weights array"""
return self._weights
def calculate_neuron_output(self, neuron, input_pattern):
"""Calculate the output of the given neuron"""
num_neurons = len(input_pattern)
s = 0.0
for j in range(num_neurons):
s += self._weights[neuron][j] * input_pattern[j]
return 1.0 if s > 0.0 else -1.0
def run_once(self, update_list, input_pattern):
"""Iterate over every neuron and update its output"""
result = input_pattern.copy()
changed = False
for neuron in update_list:
neuron_output = self.calculate_neuron_output(neuron, result)
if neuron_output != result[neuron]:
result[neuron] = neuron_output
changed = True
return changed, result
def run(self, input_pattern, max_iterations=10):
"""Run the network using the input data until the output state doesnt change
or a maximum number of iteration has been reached."""
iteration_count = 0
result = input_pattern.copy()
update_list=[]
for i in range(self._num_inputs):
update_list.append(i)
while True:
#update_list = range(self._num_inputs)
shuffle(update_list)
changed, result = self.run_once(update_list, result)
if not changed or iteration_count == max_iterations:
return result
额外的函数
def calculate_weight(i, j, patterns):
"""Calculate the weight between the given neurons"""
num_patterns = len(patterns)
s = 0.0
for mu in range(num_patterns):
s += patterns[mu][i] * patterns[mu][j]
w = (1.0 / float(num_patterns)) * s
return w
def calculate_neuron_weights(neuron_index, input_patterns):
"""Calculate the weights for the givven neuron"""
num_patterns = len(input_patterns)
num_neurons = len(input_patterns[0])
weights = np.zeros(num_neurons)
for j in range(num_neurons):
if neuron_index == j: continue
weights[j] = calculate_weight(neuron_index, j, input_patterns)
return weights
def hebbian_training(network, input_patterns):
"""Train a network using the Hebbian learning rule"""
n = len(input_patterns)
num_neurons = len(input_patterns[0])
weights = np.zeros((num_neurons, num_neurons))
for i in range(num_neurons):
weights[i] = calculate_neuron_weights(i, input_patterns)
network.set_weights(weights)





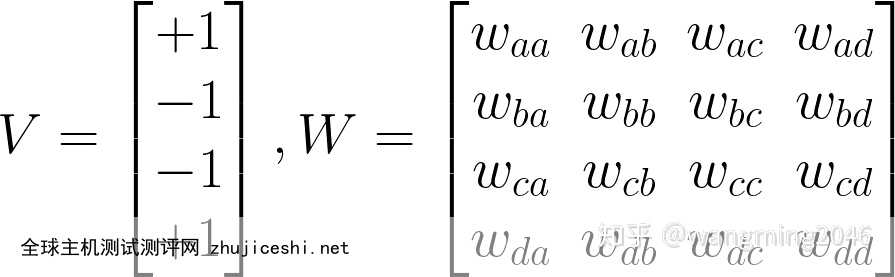

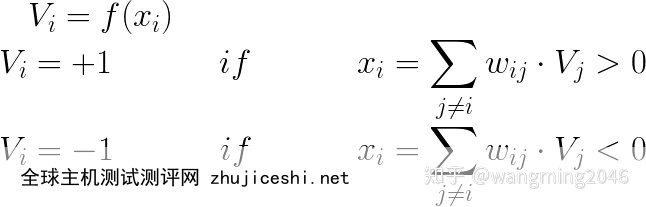










0 留言