写这篇文章的目的是因为自己在学习脉冲压缩的过程中始终不理解为啥就把脉宽给压缩了???手头的书上也没有讲清楚这个事情,正好借着实验课把整个的原理到仿真都进行梳理,虽说适用范围比较有限,但个人觉得代码中的细节和理论思想还是值得咱们雷达初学者仔细研究来入门的。另外,代码中缺少前端的数字下变频,以及后续的加窗处理(加窗会带来匹配滤波的损失,进而引出非线性调频的处理方法),都是可以进行改进完善的部分。不过,学弟学妹拿去入门或者水水作业,那还是够用啦!
下面是原创正文pdf截图,全文手敲,觉得有帮助的同学们还请抬手赏个赞赏喜欢咯!
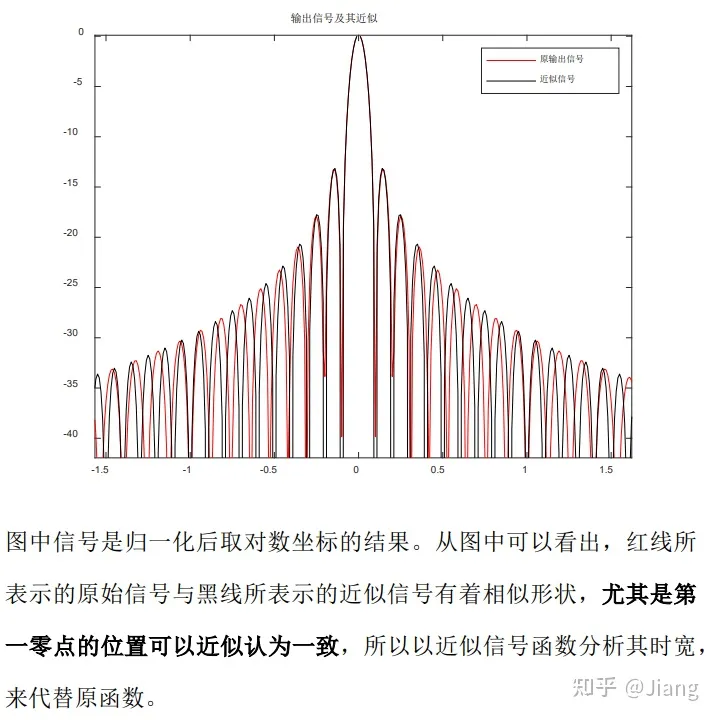
(注:20220815补充:其实这一近似过程的最终结果与“驻定相位原理”推导出的结论一致,而“驻定相位原理”给出了一种解决复杂积分问题的通用近似解法,并给出了近似条件,在脉冲压缩这个物理背景下即为时宽带宽积 >>1,且该值越大,上图两个曲线越接近。这里由于该积分式可求,所以“驻定相位原理”具体推导过程不再补充。)
以上就是所有的分析啦,下面附上利用脉冲压缩进行多个目标回波检测的代码,代码内的图片都打上了标题,可以自己复制仿真验证一下,这里就不贴过多的图片了。
%%单个目标回波的脉冲压缩
clear
clc
%%
%%仿真参数设置
fc=10e9; %载波频率
Tp=10e-6; %脉冲宽度
B=10e6; %信号带宽,理论分辨率为15m
Fs=100e6;Ts=1/Fs; %采样频率及周期
R=[1000,4960,5000,5020,5040,9000]; %目标距离
RCS=[1 1 1 1 1 1]; %反射系数,与目标数目一致
L=length(R);
C=3e8; %光速
K=B/Tp; %调频率
Rmin=1e3;Rmax=10e3; %回波测距范围
%%
%%chirp信号构造
N=ceil(Tp/Ts);
t=linspace(-Tp/2,Tp/2,N); %chirp信号模型的时间轴(默认矩形窗)
s_chirp_t=exp(1j*pi*K*t.^2); %chirp原始信号时域模型(无载频)
% freq = linspace(-Fs/2,Fs/2,N); %频域轴
% S_chirp_w=fftshift(fft(s_chirp_t,N));%将(0,2pi)内的fft转换到(-pi,pi),并以实际频率为轴
%figure,plot(freq/1e6,abs(S_chirp_w) ),xlabel(f /MHz),ylabel(幅度谱),title(Chirp信号 幅度谱);
%figure,plot(freq/1e6,unwrap(angle(S_chirp_w))*180/pi),xlabel(f /MHz),ylabel(相位谱),title(Chirp信号 相位谱);
%%
%%chirp信号回波(带有载波)
Rwind=Rmax-Rmin;
Twind=2*Rwind/C;
Nwind=ceil(Twind/Ts);
tr=linspace(2*Rmin/C,2*Rmax/C,Nwind); %可检测到的时间范围(由距离决定),时间轴
td=ones(L,1)*tr-2*R/C*ones(1,Nwind); %回波时间变量
%将L路回波叠加在一起
Srt=RCS*((abs(td)<Tp/2).*exp(1j*2*pi*fc*td+1j*pi*K*td.^2));%fc载波调制,回波加矩形窗,Nwind点,但只有N个点有值(2*(Rmin-R)/C,2*(Rmax-R)/C,Nwind)
figure,plot(tr/1e-6,real(Srt)),xlabel(t/us),ylabel(幅度),title(Chirp回波信号实部);
Srw=fftshift(fft(Srt));
freq = linspace(-Fs/2+fc,Fs/2+fc,Nwind); %频域轴
figure,plot(freq/1e6,abs(Srw)),xlabel(f /MHz),ylabel(带有载波的幅度谱),title(Chirp信号带载波);
% Srt=RCS*(abs(td)<Tp/2).*exp(1j*pi*K*td.^2);%无载波调制,回波加矩形窗,Nwind点,但只有N个点有值(2*(Rmin-R)/C,2*(Rmax-R)/C,Nwind)
%%
%%回波解调
Srt_unmodulate=Srt.*exp(-1j*2*pi*fc*tr);
figure,plot(tr/1e-6,real(Srt_unmodulate)),xlabel(t/us),ylabel(幅度),title(Chirp信号解调后实部);
%%
%%匹配滤波器构造
h_filter_t=conj(fliplr(s_chirp_t)); %时间反转取共轭构造匹配滤波器,(-Tp/2,Tp/2,N)
%%
%%脉冲压缩
%%s_output_t1=conv(Srt,h_filter_t);%时域卷积方法效率太低,为此以下采用fft实现快速卷积
%%Srt长度为Nwind,但只有N个非零值;h_filter_t长度为N。总长度可认为是Nwind+N-1
Nfft=2^nextpow2(N+Nwind-1); %圆周卷积代替线性卷积的点数条件
H_filter_w=fftshift(fft(h_filter_t,Nfft));
Srw_unmodulate=fftshift(fft(Srt_unmodulate,Nfft));
figure,plot(linspace(-Fs/2,Fs/2,Nfft)/1e6,abs(Srw_unmodulate)),xlabel(f/MHz),ylabel(幅度),title(Chirp信号解调后频谱);
S_output_w=H_filter_w.*Srw_unmodulate; %匹配滤波
s_output_ifft=ifft(S_output_w); %时域压缩后的结果
s_output_t=s_output_ifft(1:N+Nwind-1); %取(1:N+Nwind-1)个点即为线性卷积的结果,以此用fft实现快速卷积
t_conv=linspace(2*Rmin/C-Tp/2,2*Rmax/C+Tp/2,N+Nwind-1);%快速卷积后所处的时间轴
r_conv=t_conv*C/2; %时间轴转化为距离轴
%%
%%绘图
figure
subplot(1,2,1)
plot(tr/1e-6,real(Srt_unmodulate)),xlabel(t/us),ylabel(回波),title(Chirp信号 回波);%以tr作为时间轴
subplot(1,2,2)
plot(r_conv,20*log10(abs(s_output_t))),xlabel(距离/m),ylabel(幅度),title(脉冲压缩输出);
最后说一下,自己为啥不直接在知乎里输入文字,而是用pdf截图来解释原理。起初是因为不了解知乎要求markdown格式,后来发现这样截图能比较大程度得防止文章直接出现在同学们的作业里。为了方便学习,代码就直接分享给大家啦,还是希望学弟学妹认真钻研,鱼可以摸,代码可以抄,但是原理一定要自己明白!
文章链接:






















0 留言